Sebagai salah satu dasar dalam matematika dan dunia komputer, pemahaman tentang konversi bilangan Oktal ke basis bilangan lainnya adalah kunci penting. Dalam artikel ini, kita akan membahas cara konversi bilangan Oktal ke dalam tiga basis bilangan yang umum digunakan: Desimal, Binner, dan heksadesimal. Sebelum kita masuk ke teknik konversi, mari kita pahami terlebih dahulu apa itu masing-masing basis bilangan ini.
Sistem Bilangan Desimal (basis 10)
Sistem bilangan desimal adalah basis bilangan yang paling umum digunakan manusia kehidupan sehari-hari. Dalam sistem ini, kita memiliki sepuluh digit yang kita gunakan: 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Misalnya, angka 1234 dalam sistem desimal mewakili 1 ribuan, 2 ratusan, 3 puluhan, dan 4 satuan.
Sistem Bilangan Biner (Basis 2)
Sistem bilangan biner adalah basis bilangan yang paling umum digunakan dalam komputer. Dalam sistem ini, kita hanya memiliki dua digit: 0 dan 1. Ini sejalan dengan cara komputer bekerja, di mana setiap informasi diungkapkan sebagai kombinasi 0 dan 1. Angka biner sering digunakan dalam pemrograman, representasi data digital, dan komunikasi komputer.
Sistem Bilangan Oktal (Basis 8)
Sistem bilangan oktal adalah basis bilangan yang lebih jarang digunakan, tetapi masih memiliki peran dalam beberapa aplikasi. Dalam sistem ini, kita memiliki delapan digit: 0, 1, 2, 3, 4, 5, 6, dan 7. Pada dasarnya, sistem oktal adalah perpanjangan dari sistem biner, di mana tiga digit biner digunakan untuk menggantikan satu digit oktal.
Sistem Bilangan Heksadesimal (Basis 16)
Sistem bilangan heksadesimal adalah basis bilangan yang sering digunakan dalam dunia komputer, terutama dalam hal representasi data yang lebih kompleks. Dalam sistem ini, kita memiliki enam belas digit: 0-9 dan A-F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Cat. Untuk Hexadesimal Jika nanti hasil konversinya adalah rentang nilai 10 – 15, Maka ganti dengan huruf abjad sebagai berikut: A, B, C, D, E, F
A=10, B=11, C=12, D=13, E=14, F=15.Cara Konversi : Tiap digit Bilangan Oktal dikali dengan delapan sesuai posisinya, lalu tiap digitnya dipangkat mulai pangkat 0 (Nol) dari kanan.
Sebagai contoh bilangan Oktal 3243x8 pangkat 2 = 192
2x8 pangkat 1 = 16
4x8 pangkat 0 = 4
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
192 + 16 + 4 = 212
Maka Bilangan Oktal 324 Desimalnya adalah = 212
Konversi Bilangan Oktal ke Bilangan Binner
Cara Konversi : Tiap digit bilangan Oktal dikonversi ke tiga digit bilangan Biner. Sebagai contoh bilangan Oktal 324
Dari contoh diatas tiap digit Bilangan oktal dikonvers ke tiga digit bilangan biner. Sehingga hasil konversinya sebagai berikut:
Oktal 3 binernya = 011Oktal 2 binernya = 010
Oktal 4 binernya = 100
Cat. Untuk bilangan oktal 3 dan 2 hanya mendapatkan dua digit biner setelah dikonversi karena kita butuh tiga digit biner maka tambahkan angka 0 didepan.
Jadi bilangan oktal 324 binernya adalah 11010100 atau 011010100.
Konversi Bilangan Oktal ke Bilangan Hexadesimal
Cara Konversi : Untuk konversi bilangan Oktal ke Hexadesimal menggunakan dua kali konversi kebasis bilangan yaitu:
- Oktal ke Biner: Tiap digit bilangan Oktal di konversi ke tiga digit bilangan Biner terlebih dahulu menggunakan konversi oktal ke biner.
- Biner ke Hexadesimal: Kumpulkan empat digit bilangan Biner yang merupakan hasil konversi oktal ke biner dimulai digit paling kanan.
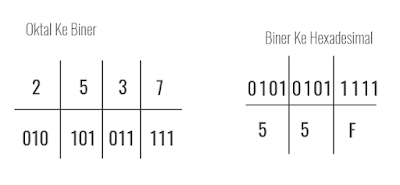
Dari contoh diatas tiap digit bilangan oktal 2537 dikonversi ke tiga digit bilangan biner terlebih dahulu sehingga akan mendapatkan hasil sebagai berikut:
2 binernya = 0105 binernya = 101
3 binernya = 011
7 binernya = 111
Jadi Bilangan Oktal 2537 binernya adalah: 010101011111
Selanjutnya bilangan Biner yang merupakan hasil konversi oktal ke biner dikumpulkan empat digit dimulai dari digit paling kanan untuk konversi biner ke hexadesimal.
0101 Hexadesimal = 5
1111 Hexadesimal = F
Jadi Bilangan Oktal 2537 Hexadesimal = 55F




.jpg)
Tidak ada komentar
Posting Komentar