Sebagai salah satu dasar dalam matematika dan dunia komputer, pemahaman tentang konversi bilangan desimal ke basis bilangan lainnya adalah kunci penting. Dalam artikel ini, kita akan membahas cara konversi bilangan desimal ke dalam tiga basis bilangan yang umum digunakan: biner, oktal, dan heksadesimal. Sebelum kita masuk ke teknik konversi, mari kita pahami terlebih dahulu apa itu masing-masing basis bilangan ini.
Sistem Bilangan Desimal (basis 10)
Sistem bilangan desimal adalah basis bilangan yang paling umum digunakan manusia kehidupan sehari-hari. Dalam sistem ini, kita memiliki sepuluh digit yang kita gunakan: 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Misalnya, angka 1234 dalam sistem desimal mewakili 1 ribuan, 2 ratusan, 3 puluhan, dan 4 satuan.
Sistem Bilangan Biner (Basis 2)
Sistem bilangan biner adalah basis bilangan yang paling umum digunakan dalam komputer. Dalam sistem ini, kita hanya memiliki dua digit: 0 dan 1. Ini sejalan dengan cara komputer bekerja, di mana setiap informasi diungkapkan sebagai kombinasi 0 dan 1. Angka biner sering digunakan dalam pemrograman, representasi data digital, dan komunikasi komputer.
Sistem Bilangan Oktal (Basis 8)
Sistem bilangan oktal adalah basis bilangan yang lebih jarang digunakan, tetapi masih memiliki peran dalam beberapa aplikasi. Dalam sistem ini, kita memiliki delapan digit: 0, 1, 2, 3, 4, 5, 6, dan 7. Pada dasarnya, sistem oktal adalah perpanjangan dari sistem biner, di mana tiga digit biner digunakan untuk menggantikan satu digit oktal.
Sistem Bilangan Heksadesimal (Basis 16)
Sistem bilangan heksadesimal adalah basis bilangan yang sering digunakan dalam dunia komputer, terutama dalam hal representasi data yang lebih kompleks. Dalam sistem ini, kita memiliki enam belas digit: 0-9 dan A-F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Cat. Untuk Hexadesimal Jika nanti hasil konversinya adalah rentang nilai 10 – 15, Maka ganti dengan huruf abjad sebagai berikut: A, B, C, D, E, F
A=10, B=11, C=12, D=13, E=14, F=15.
Cara Konversi Bilangan Desimal ke Biner
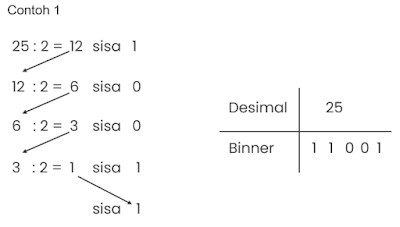
Untuk mengonversi bilangan desimal ke biner, kita perlu membagi bilangan desimal tersebut dengan angka 2 (dua) sampai habis, dengan catatan jika ada sisa bagi tulis 1 (satu) dan jika pas dibagi tulis 0. Sisa ini yang nanti akan menjadi bilangan biner. Sebagai contoh kita punya bilangan desimal 25.
Karna dibaris keempat 3:2=1 dan sudah habis dibagi maka tinggal turunkan nilai terakhir yaitu angka 1 sebagai sisa.
Maka bilangan biner dari desimal 25 = 11001
catatan: Pengambilan hasil sisa bagi diambil dari bawah keatas.
Contoh kedua anggaplah kita punya bilangan desimal 20
Karna dibaris keempat 2:2=1 dan sudah habis dibagi maka tinggal turunkan nilai terakhir yaitu angka 1 sebagai sisa.
Maka bilangan biner dari desimal 20 = 10100
catatan: Pengambilan hasil sisa bagi diambil dari bawah keatas.
Cara Konversi Bilangan Desimal ke Oktal
Proses konversi bilangan desimal ke oktal mirip dengan konversi desimal ke biner. Untuk konversi bilangan desimal ke oktal, kita perlu membagi bilangan desimal tersebut dengan angka delapan (8) sampai habis, dengan catatan jika ada sisa bagi ditulis dan jika pas dibagi tulis 0. Sisa ini yang nanti akan menjadi bilangan oktal. Sebagai contoh kita punya bilangan desimal 385.
Karna dibaris kedua 48:8=6 dan sudah habis dibagi maka tinggal turunkan nilai terakhir yaitu angka 6 sebagai sisa.
Maka bilangan oktal dari desimal 385 = 601
Cat: Untuk menghitung sisa oktal anda bisa melakukan hal sebaliknya dengan menggunakan rumus Hasil bagi x Pembagi – Nilai
Sebagai contoh dibaris pertama diatas:
Contoh kedua anggaplah kita punya bilangan desimal: 537
Cara Konversi Bilangan Desimal ke Heksadesimal
Proses konversi bilangan desimal ke Hexadesimal mirip dengan konversi desimal ke biner dan desimal ke oktal. Untuk konversi bilangan desimal ke hexadesimal, kita perlu membagi bilangan desimal tersebut dengan angka enambelas (16) sampai habis, dengan catatan jika ada sisa bagi ditulis dan jika pas dibagi tulis 0. Sisa ini yang nanti akan menjadi bilangan hexadesimal. Sebagai contoh kita punya bilangan desimal 1583.
Karna dibaris kedua 98:16=6 dan sudah habis dibagi maka tinggal turunkan nilai terakhir yaitu angka 6 sebagai sisa.
Jadi bilangan heksadesimal dari desimal 1583 = 62f
Kenapa hasilnya 62f bukan 62 15? Karna dalam bilangan hexadesimal tidak ada angka 15. Angka 15 ditulis dengan F
Contoh kedua anggaplah kita punya bilangan desimal 2840
Pentingnya Pemahaman Konversi Bilangan
Pemahaman tentang konversi bilangan dari desimal ke basis lain adalah penting dalam pemrograman, pemrosesan data, dan pengembangan perangkat lunak. Hal ini memungkinkan kita untuk beroperasi dengan data dalam berbagai format dan memahami cara komputer berkomunikasi dengan manusia dalam bahasa bilangan lain.
Dalam dunia teknologi yang semakin kompleks, pemahaman tentang dasar-dasar seperti konversi bilangan adalah langkah awal yang penting untuk memahami dan menguasai teknologi yang mengelilingi kita. Semoga artikel ini membantu Anda memahami konsep konversi bilangan Desimal ke Basis bilangan biner, oktal dan hexadesimal.
Video untuk Konversi Bilangan Desimal: Biner, Oktal dan Hexadesimal











Tidak ada komentar
Posting Komentar