Konversi Bilangan Biner: Desimal, Oktal dan Hexadesimal
Sebagai salah satu dasar dalam matematika dan dunia komputer, pemahaman tentang konversi bilangan Biner ke basis bilangan lainnya adalah kunci penting. Dalam artikel ini, kita akan membahas cara konversi bilangan binner ke dalam tiga basis bilangan yang umum digunakan: Desimal, oktal, dan heksadesimal. Sebelum kita masuk ke teknik konversi, mari kita pahami terlebih dahulu apa itu masing-masing basis bilangan ini.
Sistem Bilangan Desimal (basis 10)
Sistem bilangan desimal adalah basis bilangan yang paling umum digunakan manusia kehidupan sehari-hari. Dalam sistem ini, kita memiliki sepuluh digit yang kita gunakan: 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Misalnya, angka 1234 dalam sistem desimal mewakili 1 ribuan, 2 ratusan, 3 puluhan, dan 4 satuan.
Sistem Bilangan Biner (Basis 2)
Sistem bilangan biner adalah basis bilangan yang paling umum digunakan dalam komputer. Dalam sistem ini, kita hanya memiliki dua digit: 0 dan 1. Ini sejalan dengan cara komputer bekerja, di mana setiap informasi diungkapkan sebagai kombinasi 0 dan 1. Angka biner sering digunakan dalam pemrograman, representasi data digital, dan komunikasi komputer.
Sistem Bilangan Oktal (Basis 8)
Sistem bilangan oktal adalah basis bilangan yang lebih jarang digunakan, tetapi masih memiliki peran dalam beberapa aplikasi. Dalam sistem ini, kita memiliki delapan digit: 0, 1, 2, 3, 4, 5, 6, dan 7. Pada dasarnya, sistem oktal adalah perpanjangan dari sistem biner, di mana tiga digit biner digunakan untuk menggantikan satu digit oktal.
Sistem Bilangan Heksadesimal (Basis 16)
Sistem bilangan heksadesimal adalah basis bilangan yang sering digunakan dalam dunia komputer, terutama dalam hal representasi data yang lebih kompleks. Dalam sistem ini, kita memiliki enam belas digit: 0-9 dan A-F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Cat. Untuk Hexadesimal Jika nanti hasil konversinya adalah rentang nilai 10 – 15, Maka ganti dengan huruf abjad sebagai berikut: A, B, C, D, E, F
A=10, B=11, C=12, D=13, E=14, F=15.
Konversi Bilangan Biner ke Bilangan Desimal
Konversi Bilangan Biner ke bilangan desimal, dengan cara bilangan biner dikalikan masing-masing digit sesuai dengan posisinya dan berikan pangkat tiap digit mulai pangkat 0 dari kanan. Contoh bilangan biner 1101.
Kita akan gunakan rumus seperti berikut:
Pertama ambil tiap digit dari bilangan biner dari kiri kekanan kalikan dengan angka dua tiap digit bilangan biner, kemudian berikan pangkat tiap-tiap angka dua mulai pangkat Nol dari kanan, kemudian hitung hasil perkalian pangkat tersebut dan hasilnya dijumlahkan.
Dari contoh diatas merupakan hasil perkalian pangkat:
1x2 pangkat 4 = 16
1x2 pangkat 3 = 8
0x2 pangkat 2 = 0
0x2 pangkat 1 = 0
1x2 pangkat 0 = 1
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
16 + 8 + 0 + 0 + 1 = 25
Maka Bilangan Biner 11001 Desimalnya adalah = 25
Contoh selanjutnya anggaplah kita punya bilangan Binner 1000001
Dari contoh diatas merupakan hasil perkalian pangkat:
1x2 pangkat 6 = 64
0x2 pangkat 5 = 0
0x2 pangkat 4 = 0
0x2 pangkat 3 = 0
0x2 pangkat 2 = 0
0x2 pangkat 1 = 0
1x2 pangkat 0 = 1
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
64+0+0+0+0+0+1 = 65
Konversi Bilangan Biner ke Bilangan Oktal
Untuk konversi bilangan Biner ke bilangan oktal, dengan cara mengumpulkan 3 digit bilangan biner mulai dari digit paling kanan kemudian lakukan konversi bilangan biner ke desimal Contoh bilangan biner 110101.
Dari contoh diatas Bilangan Biner 110101 kumpulkan 3 digit bilangan biner dari kanan kekiri. 3 digit pertama dari kanan adalah 101 dan 3 digit berikutnya adalah 110 Setelah itu lakukan konversi bilangan biner ke desimal dari bilangan biner 110 dan 101:
Biner 110
1x2 pangkat 2 = 4
1x2 pangkat 1 = 2
0x2 pangkat 0 = 0
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
4+2+0 = 6
Kemudian Biner 101
1x2 pangkat 2 = 4
0x2 pangkat 1 = 0
1x2 pangkat 0 = 1
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
4+0+1 = 5
Maka Bilangan Biner 110101 Oktalnya adalah = 65 (enam lima)
Contoh berikutnya anggaplah kita punya bilangan Binner 1000001
Cat. Berdasarkan contoh diatas kita diharuskan mengumpulkan 3 digit bilangan binner 3 digit di kanan adalah 001, 3 digit ditengah 000 dan masih tersisa 1 digit lagi bilangan binner di kiri. Karena kita butuh 3 digit maka tambahkan dua nol didepan angka 1 sehingga menjadi 3 digit 001. Jadi intinya disini jika tidak cukup tiga digit terakhir maka tambahkan Nol didepan.
Konversi Bilangan Biner ke Bilangan Hexadesimal
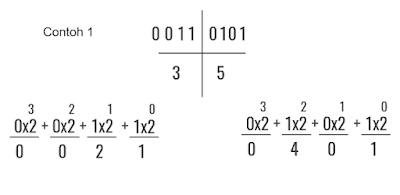
Untuk konversi bilangan Biner ke bilangan Hexadesimal, dengan cara mengumpulkan 4 digit bilangan biner mulai dari digit paling kanan kemudian lakukan konversi bilangan biner ke desimal caranya sama ketika konversi bilangan biner ke oktal hanya saja jumlah digit yang dikumpulkan adalah 4. sebagai contoh kita punya bilangan Binner 110101
Dari contoh diatas Bilangan Biner 110101 kumpulkan 4 digit bilangan biner dari kanan kekiri. 4 digit pertama dari kanan adalah 0101 dan 4 digit berikutnya adalah 0011. Kenapa 0011 karena kita menambahkan dua angka nol didepan hal ini dilakukan untuk mencukupkan 4 digit.
Setelah itu lakukan konversi bilangan biner ke desimal dari bilangan biner 0011 dan 0101:
Biner 0011
0x2 pangkat 3 = 0
0x2 pangkat 2 = 0
1x2 pangkat 1 = 2
1x2 pangkat 0 = 1
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
0+0+2+1 = 3
Kemudian Biner 0101
0x2 pangkat 3 = 0
1x2 pangkat 2 = 4
0x2 pangkat 1 = 0
1x2 pangkat 0 = 1
Selanjutnya hasil perkalian pangkat tersebut dijumlahkan:
0+4+0+1 = 5
Maka Bilangan Biner 110101 Hexadesimalnya adalah = 35 (Tiga lima)
Video mengenai konversi bilangan binner ke basis bilangan yang lain:


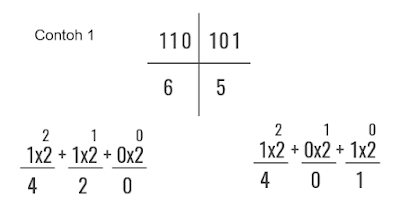



.jpg)

Tidak ada komentar
Posting Komentar